Question

6. At a bus interchange, a number of passengers boarded a bus. At the first

bus stop, of the passengers alighted the bus and 6 people boarded the
bus. At the 2nd bus stop, of the passengers alighted and 10 passengers
boarded the bus. There were 24 passengers on the bus when it left the
2nd bus stop. How many passengers boarded the bus at the interchange?​

Answer 1

The answer is given below

Explanation:

Let the number of passengers that boarded the bus at the interchange be x.

At the first bus stop, 1/4 of the passengers alighted the bus and 6 people boarded the bus.

Therefore The number of passengers when the bus left the first bus stop =
`x-(1)/(4)x +6=(3)/(4)x+6`

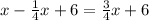
At the 2nd bus stop, 8/15 of the passengers alighted and 10 passengers boarded the bus.

Therefore The number of passengers when the bus left the second bus stop

`=(3)/(4)x+6-(8)/(15)( (3)/(4)x+6)+10=(3)/(4)x+6-(8)/(20)x-3.2+10\\\\=(7)/(20)x+12.8`

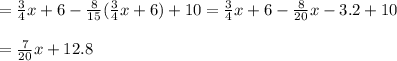
Given that there were 24 passengers on the bus when it left the 2nd bus stop

`(7)/(20)x+12.8=24\\7x+256=480\\7x=480-256\\7x=224\\x=32`

Therefore 32 passengers boarded the bus at the interchange