Question

Two random samples with sizes 100 and n are chosen from the populations with the means 85.6 and 82.1. They have standard deviations 12.4 and 8.9, respectively. Which of these values of n would result in the smallest SE?

a. 100
b. 120
c. 90
d. 50
e. 70

Answer 1

`SE= \sqrt{(\sigma^2_1)/(n_1)+(\sigma^2_2)/(n_2)}`

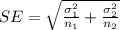
And for this case if we have the same sample size we got the minimum value when we have the higher value fo n for each one and for this case would be the answer:

b. 120

Explanation:

For this case we have the following info given:

`n_1 = n_2 = 100`

`\mu_1 = 85.6`

`\mu_2 = 82.1`

`\sigma_1 =12.4`

`\sigma_2 = 8.9`

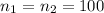
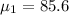
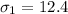
We assume that the variable of interest is the linear combination of the two means and for this case the standard error would be given by:

`SE= \sqrt{(\sigma^2_1)/(n_1)+(\sigma^2_2)/(n_2)}`

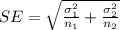
And for this case if we have the same sample size we got the minimum value when we have the higher value fo n for each one and for this case would be the answer:

b. 120