Answer:
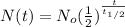
Where
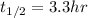 represent the half life and the intial amount would be
represent the half life and the intial amount would be
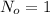
And we want to find the time in order to have a 95% of decay so we can set up the following equation:

If we apply natural log on both sides we got:
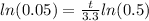
And solving for t we got:
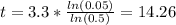
So then would takes about 14.26 hours in order to have 95% of the lead to decay
Explanation:
For this case we can define the variable of interest amount of Pb209 and for the half life would be given:
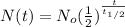
Where
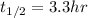 represent the half life and the intial amount would be
represent the half life and the intial amount would be
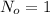
And we want to find the time in order to have a 95% of decay so we can set up the following equation:

If we apply natural log on both sides we got:
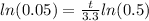
And solving for t we got:
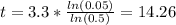
So then would takes about 14.26 hours in order to have 95% of the lead to decay