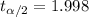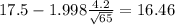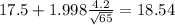Question

Sales personnel for Skillings Distributors submit weekly reports listing the customer contacts made during the week. A sample of 65 weekly reports showed a sample mean of 17.5 customer contacts per week. The sample standard deviation was 4.2.

Required:
Provide 90%90% and 95%95% confidence intervals for the population mean number of weekly customer contacts for the sales personnel.

Answer 1

Since the Confidence is 0.90 or 90%, the value of
`\alpha=0.1` and
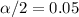`\alpha/2 =0.05`, and the critical value would be
`t_(\alpha/2)=1.669`

And replacing we got

`17.5-1.669(4.2)/(√(65))=16.63`

`17.5+1.669(4.2)/(√(65))=18.37`

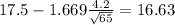
For the 95% confidence the critical value is
`t_(\alpha/2)=1.998`

`17.5-1.998(4.2)/(√(65))=16.46`

`17.5+1.998(4.2)/(√(65))=18.54`

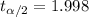
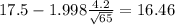
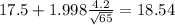
Explanation:

Information given

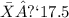`\bar X¿ 17.5` represent the sample mean

`\mu` population mean (variable of interest)

s¿4.2 represent the sample standard deviation

n¿65 represent the sample size

Confidence interval

The confidence interval for the mean is given by the following formula:

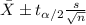`\bar X \pm t_(\alpha/2)(s)/(√(n))` (1)

The degrees of freedom are given by:

`df=n-1=65-1=64`

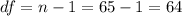
Since the Confidence is 0.90 or 90%, the value of
`\alpha=0.1` and
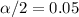`\alpha/2 =0.05`, and the critical value would be
`t_(\alpha/2)=1.669`

And replacing we got

`17.5-1.669(4.2)/(√(65))=16.63`

`17.5+1.669(4.2)/(√(65))=18.37`

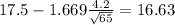
For the 95% confidence the critical value is
`t_(\alpha/2)=1.998`

`17.5-1.998(4.2)/(√(65))=16.46`

`17.5+1.998(4.2)/(√(65))=18.54`