Question

A solid wooden door, 90 cm wide by 2.0 m tall, has a mass of 35 kg. It is open and at rest. A small 500-g ball is thrown perpendicular to the door with a speed of 20 m/s and hits the door 60 cm from the hinged side, causing it to begin turning. The ball rebounds along the same line with a speed of 16.0 m/s relative to the ground.

Required:
How much energy is lost during this collision?

a. 15J
b. 16J
c. 13J
d. 4.8J
e. 30J

Answer 1

the kinetic energy lost in the collison is a) 30 J

Step-by-step explanation:

given data

mass of door m1 = 35 kg

width a = 90 cm = 0.9 m

the mass of ball m2 = 500 g = 0.5 kg

initial speed of ball u = 20 m/s

final speed of ball v = 16 m/s

r = 60 cm = 0.6 m

soluion

we will consider here final angular speed of the door = w

so now we use conservation of angular momentum that is

Li = Lf ........................1

that is express as

m2 × u × r = I × w + m2 × v × r

put here value and we get

0.5 × 20 × 0.6 =
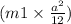`(m1 * (a^2)/(12))` × w + 0.5 × 16 × 0.6

solve it we get

w = 0.508 rad/s

so that here

the kinetic energy lost in the collison,

KE = KE initial - KE final ..................2

put here value

KE = 0.5 × m2 × u² - (0.5 × I × w² + 0.5 × m2 × v²)

KE = 0.5 × (0.5 × 20² - (35 × 0.9² ÷ 12) × 0.508² - 0.5 × 16²) J

KE = 30 J

the kinetic energy lost in the collison is a) 30 J