Question

4)

If the first three Fibonacci numbers are x, = 1, .x = 1, x3 = 2,
what is the value of n for which .x. +x... + x = 68?

Answer 1

The value of n for which xₙ₋₂ + xₙ₋₁ + xₙ = 68 is n = 9

Explanation:

The nth term of Fibonacci number is given by the following relation;

`F_n = ((1 + √(5) )^n - (1 - √(5) )^n )/(2^n√(5) )`

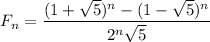
Given that we have ;

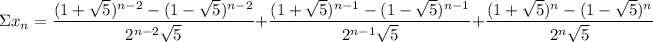`\Sigma x_n = ((1 + √(5) )^(n-2) - (1 - √(5) )^(n-2) )/(2^(n-2)√(5) ) + ((1 + √(5) )^(n-1) - (1 - √(5) )^(n-1) )/(2^(n-1)√(5) )+((1 + √(5) )^(n) - (1 - √(5) )^(n) )/(2^(n)√(5) )`When n = 3, we have;

∑xₙ = 4

When n = 4 we have

∑xₙ = 4

When n = 6 we have

∑xₙ = 16

When n = 9 we have

∑xₙ = 68

Therefore, we have the value of n for which xₙ₋₂ + xₙ₋₁ + xₙ = 68 is n = 9.