Answer:

Explanation:
Hello,
step 1 - we divide all terms by 2
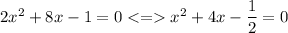
step 2 - we complete the square
we can notice that
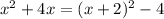
so
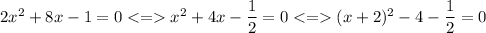
step 3 - we move the constant term to the right of the equation
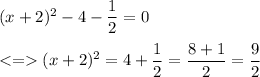
step 4 - we take the square root on both sides of the equation
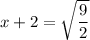
or

step 5 - we subtract 2 from both sides
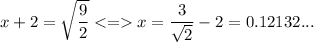
or
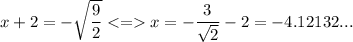
so the solutions are 0.12 and -4.12
hope this helps