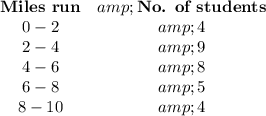Question

Use the raw data below to create a table that can be used to create a histogram with 5

classes. Assume the data is the miles ran by students in our class.
{3.5, 2.7, 1.6, 2.9, 1.7, 5.3, 7.5, 8.2, 4.6, 1.3,
4.7, 9.4, 7.6, 3.9, 3.2, 8.1, 4.9, 5.7, 2.6, 3.2,
6.5, 4.8, 3.5, 4.8, 9.2, 4.9, 1.1, 2, 6.4, 7.1}
Define the Number of Classes we need for our histogram.
We will have
classes. We will have ______ classes

Answer 1

Five classes

Explanation:

1. Sort the data

You get

1.1, 1.3, 1.6, 1.7, 2, 2.6, 2.7, 2.9, 3.2, 3.2, 3.5, 3.5, 3.9, 4.6, 4.7, 4.8, 4.8, 4.9, 4.9, 5.3, 5.7, 6.4, 6.5, 7.1, 7.5, 7.6, 8.1, 8.2, 9.2, 9.4

2. Calculate the range

Range = Max - Min = 9.4 - 1.1 = 8.3

3. Calculate the class width

Divide the range by the number of classes

8.3/5 = 1.7

Round this up to 2.

4. Decide where to start the histogram

You could use classes: 1 - 3, 3 - 5, 5 - 7, 7 - 9, 9 -11

However, even numbers are easier to read.

It would be preferable to use classes: 0 - 2, 2 - 4, 4 - 6, 6 - 8, 8 - 10

5. Prepare a frequency distribution table

Note: Each class does not include its largest possible value. Thus, a value of 2 goes into Class 2 - 4, (not Class 0 - 2).

`\begin{array}{cc}\textbf{Miles run} & \textbf{No. of students} \\0 - 2 & 4 \\2 - 4 & 9 \\4 - 6 & 8 \\6 - 8 & 5 \\8 - 10 & 4 \\\end{array}`