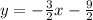Answer:
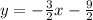
Explanation:
Let the equation of the perpendicular line is,
y = mx + b
where m = slope of the line
b = y-intercept
From the graph, slope of the line passing through (0, -1) and (3, 1),
m' =
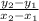
m' =
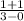
m' =
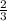
To get the slope (m) of this line we will use the property of perpendicular lines,
m × m' = (-1)
m ×
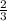 = -1
= -1
m =
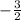
Equation of the perpendicular line will be,
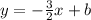
x-intercept of the line is (-3) therefore, point on the line is (-3, 0)
0 =
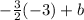
b =
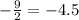
Equation of the line will be,