Question

Dependent and Independent Events

S
?
Tom is playing a board game.
He has rolled a six nine times in a row.
What's the probability that his 10th roll will not be a six?
금

Answer 1

Each roll of a dice is an independent event, thus the chances of not rolling a six on the 10th roll for Tom is the same as any single roll, specifically 5/6.

Step-by-step explanation:

The subject of this question is Mathematics, and it relates to the concept of probability in the context of dependent and independent events. In this particular scenario with Tom rolling a die, each roll is an independent event. This means the probability of rolling a specific outcome on the die is not affected by previous rolls. Therefore, the probability that Tom's 10th roll will not be a six is the same every time the die is rolled, regardless of how many sixes have been rolled previously.

For a fair, six-sided die, the sample space S is {1, 2, 3, 4, 5, 6}. Since there is only one six in the sample space, the probability of rolling a six is 1/6. Consequently, the probability of not rolling a six on a fair die is 5/6, as there are five other faces that are not a six. Thus, the probability that Tom's 10th roll will not be a six is 5/6.

Answer 2

Step-by-step explanation:

Hello!

If you consider the 6-sided dice to be balanced, then each result has the same probability of occurrence: P(1)=P(2)=P(3)=P(4)=P(5)=P(6)=
`(1)/(6)`

And each time Tom rolls the dice is independent of the other times, this means that you can disregard all previous rolls and calculate the 10nth time as if it is the 1st one.

Be the event A: "Tom rolled the dice for the 10nth time and obtained a 6"

The probability of A occurring will be P(A)= 1/6

On the other hand, the complement of "A" will be
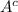`A^c`: "Tom rolled the dice for the 10nth time and didn't obtain a 6"

This means he could obtain a 1 or a 2 or a 3 or a 4 or a 5

You can calculate the probability pf this event by adding the probability of obtaining each value P(
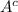`A^c`)= P(1)+P(2)+P(3)+P(4)+P(5)= 1/6*5= 5/6

Or by subtracting the probability of A to the total probability of the sample space:

P(
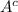`A^c`)= 1 - P(A)= 1 - 1/6= 5/6

I hope this helps!