Rewrite in simplest radical form x 5/6 x 1/6

Question

asked Mar 27, 2021 80.8k views

1 Answer

Mattias Nordberg · Answer 1 · 2021-04-02T23:22:11+0000

Answer:

$x^{(5)/(6)}/x^{(1)/(6)} = \sqrt[3]{x^2}$

Explanation:

Given

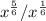
$x^{(5)/(6)}/x^{(1)/(6)}$

Required

Rewrite in simplest radical form

Using laws of indices:

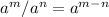
a^m/a^n = a^(m-n)

This implies that

$x^{(5)/(6)}/x^{(1)/(6)} = x^{(5)/(6) - (1)/(6)}$

Solve Exponents

$x^{(5)/(6)}/x^{(1)/(6)} = x^{(5 - 1)/(6) }$

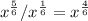
$x^{(5)/(6)}/x^{(1)/(6)} = x^{(4)/(6) }$

Simplify exponent to lowest fraction

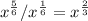
$x^{(5)/(6)}/x^{(1)/(6)} = x^{(2)/(3) }$

Using laws of indices:

$a^{(m)/(n)} = \sqrt[n]{a^m}$

This implies that

$x^{(5)/(6)}/x^{(1)/(6)} = \sqrt[3]{x^2}$

This is as far as the expression can be simplified