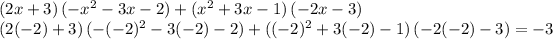Answer:
The derivative of that product of functions evaluated at the point x=-2 gives "-3"
Explanation:
Recall that the derivative of a product of two functions f(x) and g(x) is given by the formula:
(f*g)'= f' * g+ f * g'
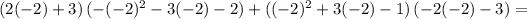
So it would be convenient to reduce this product of three functions to a product of just 2, performing (-x-1)*(x+2) = - x^2 - 2x - x -2 = - x^2 -3x -2
therefore we need to find the derivative of x^2 + 3x -1, and the derivative of - x^2 -3x -2 to obtain the answer:
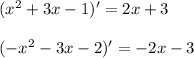
Now, applying the product rule for those two trinomial functions, we get:
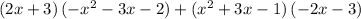
which at x = -2 becomes: