Answer:
0.894
Explanation:
Data provided in the question
BC length = 17.89 unit
DC length = 16 unit.
Now, we have to compute the angle y with the help of the cosine function;
Cosine defines the ratio between the right angle adjacent side and the hypotenuse
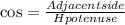
As per the triangle BDC;
Hypotenuse = BC =17.89 unit
And, the Adjacent side = 16 units
So;

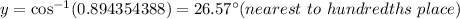
Now, determine the value of angle x
In right angle ΔABC;
As we know that
The three angles sum is 180 degrees
So,
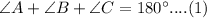
According to the given figure
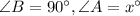
and
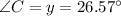
Now Substitute these in (1) for solving the angle x;

or
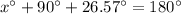
or
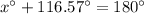
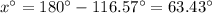
Finally we have to determine the value of sin x;
Hence,
The value of

or
= 0.894