Question

If the sum of the integers from 15 to 50,

inclusive, is equal to the sum of the integers
from n to 50, inclusive, and n<15, then n=

A)-49
B)-35
C)-15
D-14​

Answer 1

n = -15

Explanation:

Given

Sum of Integers from 15 to 50 (inclusive) = Sum of integers from n to 50 (inclusive)

n < 15

Required

Find n

We can split the given parameters to 2

i. Sum of Integers from 15 to 50 (inclusive)

ii. Sum of integers from n to 50 (inclusive)

Solving for (i): Sum of Integers from 15 to 50 (inclusive)

We'll make use of sum of n terms of an arithmetic;

This is given as follows

`S_n = (n)/(2)(T_1 + T_n)`

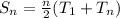
Where n is the number of terms from 15 to 50

T1 is the first term; T1 = 15

Tn is the last term; Tn = 50

n is calculated using

`n = T_n - T_1 + 1`

`n = 50 - 15 + 1`

`n = 36`

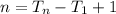
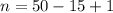
The formula becomes

`S_n = (n)/(2)(T_1 + T_n)`

`S_n = (36)/(2)(15 + 50)`

`S_n = (36)/(2)(65)`

`S_n = 18(65)`

`S_n = 1170`

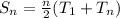
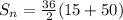
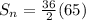
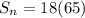
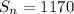
Solving for (ii): Sum of integers from n to 50 (inclusive)

We'll also make use of the same formula used above

`S_n = (n)/(2)(T_1 + T_n)`

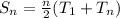
Where n is the number of terms from n to 50

T1 is the first term; T1 = n

Tn is the last term; Tn = 50

n is calculated using

`n = T_n - T_1 + 1`

`n = 50 - n + 1`

`n = 50 + 1 - n`

`n = 51 - n`

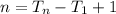
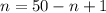
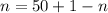
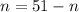
The formula becomes

`S_n = (n)/(2)(T_1 + T_n)`

`S_n = (51 - n)/(2)(n + 50)`

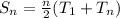
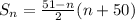
Recall that the Sum of Integers from 15 to 50 (inclusive) = Sum of integers from n to 50 (inclusive);

This implies that

Sn (i) = Sn (ii)

As such; we have

`S_n = (51 - n)/(2)(n + 50) = 1170`

`(51 - n)/(2)(n + 50) = 1170`

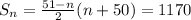
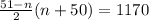
Multiply both sides by 2

`2 * (51 - n)/(2)(n + 50) = 1170 * 2`

`(51 - n)(n + 50) = 1170 * 2`

`(51 - n)(n + 50) = 2340`

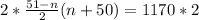
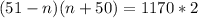
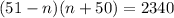
Open Brackets

`51(n + 50) - n(n + 50) = 2340`

`51*n + 51 * 50 - n * n - n * 50 = 2340`

`51n + 2550 - n^2 - 50n = 2340`

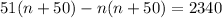
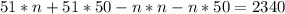
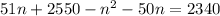
Reorder

`-n^2 + 51n - 50n + 2550 = 2340`

`-n^2 + n + 2550 = 2340`

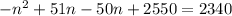
Subtract 2340 from both sides

`-n^2 + n + 2550 -2340 = 2340 -2340`

`-n^2 + n + 210 = 0`

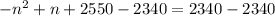
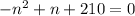
Multiply both sides by -1

`-1(-n^2 + n + 210) = -1 * 0`

`n^2 - n - 210 = 0`

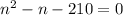
At this point, we have a quadratic equation; as such, it'd be solved as follows:

`n^2 - n - 210 = 0`

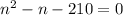
Expand

`n^2 + 15n - 14n - 210 = 0`

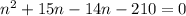
Factorize

`n(n + 15) - 14(n + 15) = 0`

`(n - 14)(n + 15) = 0`

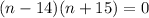
Split the above expression

`(n - 14) = 0 \ or\ (n + 15) = 0`

`n - 14 = 0 \ or\ n + 15 = 0`

`n = 14\ or\ n = -15`

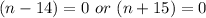
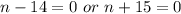
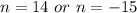
The question states that n < 15;

This means that we'll discard the value of n = 14

Hence, n = -15