Question

A political scientist wants to prove that a candidate is currently carrying more than 60% of the vote in the state. She has her assistants randomly sample 200 eligible voters in the state by telephone and only 90 declare that they support her candidate. The observed z value for this problem is _______. 4.33 2.33 0.45 -.31 -4.33

Answer 1

Z= -4.33

Explanation:

Hello!

The study variable is:

X: number of voters that support the candidate out of 200 surveyed voters.

This variable has a binomial distribution, where the "success" is that the voter supports the candidate and the "failure" is that the voter doesn't support the candidate. X~Bi(n;p)

Considering the sample size is large enough, you can apply the Central Limit Theorem and approximate the distribution of the sample proportion to normal: ^p ≈ N(p;
`(p(1-p))/(n)`)

Using this distribution you can an approximation to the standard normal distribution:
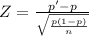`Z= \frac{p'-p}{\sqrt{(p(1-p))/(n) }}`≈N(0;1)

Where the sample proportion is ^p= p'=
`(x)/(n) = (90)/(200) = 0.45`

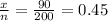
x= number of successes

n= sample size

The population proportion is p= 0.60

`Z= \frac{0.45-0.60}{\sqrt{(0.60*0.40)/(200) }}= -4.33`

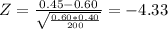
I hope this helps!