Answer:
Option (1)
Explanation:
Since the length of arc YZ = 12 units
m∠YXZ = one third of the full circle =
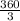 = 120°
= 120°
From the formula of arc length,
Length of arc =
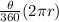
Where θ = Central angle subtended by the arc
r = radius of the circle
By substituting these values in the formula,
12 =
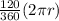
12 =
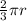

r =
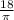
r = 5.73
r ≈ 6 units
Therefore, Option (1) will be the answer.