Question

A gas occupies a volume of 1.0 m3 in a cylinder at a pressure of 120kPa. A piston compresses the gas until the volume is 0.25m3, the temperature remaining constant. What is the new pressure of the gas?

Answer 1

Approximately
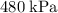`480\; \rm kPa`, assuming that this gas is an ideal gas.

Step-by-step explanation:

• Let
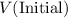  `V(\text{Initial})` and
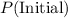  `P(\text{Initial})` denote the volume and pressure of this gas before the compression.
• Let
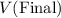  `V(\text{Final})` and
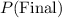  `P(\text{Final})` denote the volume and pressure of this gas after the compression.

By Boyle's Law, the pressure of a sealed ideal gas at constant temperature will be inversely proportional to its volume. Assume that this gas is ideal. By this ideal gas law:

`\displaystyle \frac{P(\text{Final})}{P(\text{Initial})} = \frac{V(\text{Initial})}{V(\text{Final})}`.

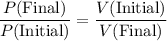Note that in Boyle's Law,
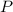`P` is inversely proportional to
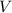`V`. Therefore, on the two sides of this equation, "final" and "initial" are on different sides of the fraction bar.

For this particular question:

• 
  `V(\text{initial}) = 1.0\; \rm m^3`.
• 
  `P(\text{Initial}) = 120\; \rm kPa`.

• 
  `V(\text{final}) = 0.25\; \rm m^3`.
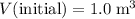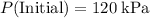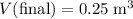• The pressure after compression,
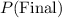  `P(\text{Final})`, needs to be found.

Rearrange the equation to obtain:

`\displaystyle P(\text{Final}) = \frac{V(\text{Initial})}{V(\text{Final})} \cdot P(\text{Initial})`.

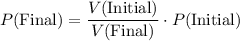Before doing any calculation, think whether the pressure of this gas will go up or down. Since the gas is compressed, collisions between its particles and the container will become more frequent. Hence, the pressure of this gas should increase.

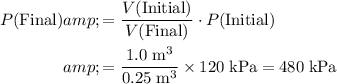`\begin{aligned}P(\text{Final}) &= \frac{V(\text{Initial})}{V(\text{Final})} \cdot P(\text{Initial})\\ &= (1.0\; \rm m^(3))/(0.25\; \rm m^(3)) * 120\; \rm kPa = 480\; \rm kPa\end{aligned}`.