Question

N = Noekt

Situation:
Find the age of the bird skeleton to the neares
year
A geologist in South America discovers a
bird skeleton that contains 67% of its
original amount of C-14.
Enter the correct answer
DE
No = inital amount of C-14 (at time
t = 0)
N
= amount of C-14 at time t
K = 0.0001
t = time, in years

Answer 1

Explanation:

You wrote the formula incorrectly. It is, correctly:

`N=N_0e^(-kt)`

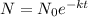
The k has to be a negative in the formula; if it's not, the time ends up as negative, which will NEVER be the case (unfortunately, time does not go backwards).

If the skeleton contains 67% of the C-14 it contained when the bird was alive, that 67 is our "N". When the bird was alive, it contained 100% of its C-14; so
`N_0` is 100. We know k, e is Euler's number, and we are looking for t.

`67=100e^(-.0001t)`

Begin by dividing both sides by 100 to get

`.67=e^{-.0001t`

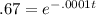
To get that t out from its current exponential position, we take the natural log of both sides. We do this because 1. it's the only way to get an exponent down from that position and 2. because natural logs and e are inverses of each other; natural logs "undo" e's and e's "undo" natural logs.

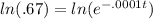`ln(.67)=ln(e^(-.0001t))` Again, because e and ln undo each other:

ln(.67) = -.0001t and solve for t. Take the natural log of .67 on your calculator and get

-.4004775666 = -.0001t and

t = 4004.7 years