Question

PLEASE HELP!!!! Seventeen consecutive positive integers have a sum of 306. What is the sum of the seventeen consecutive integers that immediately follow the seventeen positive integers that sum to 306?

Answer 1

595

Explanation:

Let the first integer be n. Then each consecutive integer will be (n+1), (n+2)... until (n+16).

First, from the formula
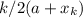`k/2(a+x_(k))`, where k is the number of elements and xk is the last element, we can find 1+2+3 ... +15+16 = (16/2)(1+16)=136.

Anyways, this means that 17n+136=306.

We can find that n=10

Thus, the first integer is 10, and the 17th integer will be 10+16=26.

Thus, the first integer immediately proceeding 26 is 27. There are a total of 17 digits including 27 so we can add 16 to 27 to find the last digit, which is 43. There are again 17 digits in this set.

Thus, we have: 17/2(27+43)=595.