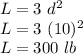Question

The maximum load a beam will support varies directly with the square of the diagonal of the beam’s cross-section. A beam with diagonal 6in will support a maximum load of 108lb. Write the equation that relates the load L to the diagonal d of the cross-section. How large of a load, in pounds, will a beam with a 10in diagonal support?

Answer 1

L=3d^2 the beam will support 300 pounds

Explanation:

108=k x 6^2

Dividing by 6^2=36 gives k=3, so an equation that relates L and d is

L=3d^2 d=10 yields

3(10)^2=300

So a beam with a 10in diagonal will support a 300lb load.

Answer 2

The equation is:

`L=3\,\,d^2\\`

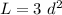
and a beam with 10 in diagonal will support 300 lb

Explanation:

The mathematical expression that represents the statement:

"The maximum load a beam will support varies directly with the square of the diagonal of the beam’s cross-section. "

can be written as:

`L=k\,\,d^2`

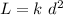
where k is the constant of proportionality

To find the constant we use the data they provide: "A beam with diagonal 6 in will support a maximum load of 108 lb.":

`L=k\,\,d^2\\108 = k\,\,(6)^2\\k=(108)/(36) \,\,(lb)/(in^2)\\ k = 3\,\,(lb)/(in^2)`

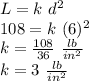
Now we can use the proportionality found above to find the maximum load for a 10 in diagonal beam:

`L=3\,\,d^2\\L=3\,\,(10)^2\\L=300 \,\,lb`