Question

A particle starts to move in a straight line from

a point with velocity 10 m/s and acceleration - 20 m/s²? Find the position and velocity of the
particle at (i) t = 5s, (ii) t' = 10 s.​

Answer 1

Answer: s(5) = -200, v(5) = -90

s(10) = -900, v(10) = -190

Step-by-step explanation:

Position: s(t)

Velocity: s'(t) = v(t) ⇒
`s(t)=\int {v(t)} \, dt`

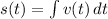
Acceleration v'(t) = a(t) ⇒
`v(t)=\int {a(t)} \, dt`

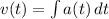
We are given that acceleration a(t) = -20 and velocity v(t) = 10

`v(t)=\int {a(t)} \, dt\\\\v(t)=\int{-20}\, dt\\\\v(t)=-20t + C \\\\v(t)=10\quad \longrightarrow \quad C=10\\\\v(t)=-20t+10`

`s(t)=\int {v(t)} \, dt\\\\s(t)=\int {(-20t+10)} \, dt\\\\s(t)=-10t^2+10t\\\\`

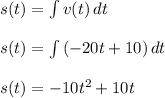
(a) Input t = 5 into the s(t) and v(t) equations

s(5) = -10(5)² + 10(5) v(5) = -20(5) + 10

= -250 + 50 = -100 + 10

= -200 = -90

(b) Input t = 10 into the s(t) and v(t) equations

s(10) = -10(10)² + 10(10) v(10) = -20(10) + 10

= -1000 + 100 = -200 + 10

= -900 = -190