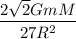Question

The centres of a ring of mass m and a sphere

of mass Mof equal radius R, are at a distance
V8 Rapart as shown. The force of attraction
between the ring and the sphere is.
Plz help me out !!!

Answer 1

Given that,

Mass of ring = m

Mass of sphere = M

Radius = R

Distance = √8R

We need to calculate the intensity of gravitational field

Using formula of intensity

`E_(g)=\frac{Gmx}{\sqrt{(r^2+x^2)^(3)/(2)}}`

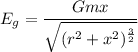
Put the value into the formula

`E_(g)=\frac{Gm√(8)R}{(R^2+8R^2)^{(3)/(2)}}`

`E_(g)=\frac{2√(2)Gm}{(9R^2)^{(3)/(2)}}`

`E_(g)=(2√(2)Gm)/(27R^2)`

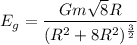
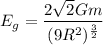
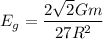
We need to calculate the force of attraction between the ring and the sphere

Using formula of attraction force

`F=M* E_(g)`

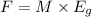
Where, M = mass of sphere

E = intensity of gravitational field

Put the value into the formula

`F=(2√(2)GmM)/(27R^2)`

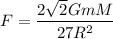
Hence, The force of attraction between the ring and the sphere is
`(2√(2)GmM)/(27R^2)`