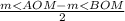Question

Point M is in the interior of angle AOB, the ray OC is a bisector of this angle. Prove that the measure of angle MOC is equal to one-half the difference of the measure of angles AOM and BOM

Answer 1

Explanation:

Given: point M,

m<AOB,

OC the bisector of m<AOB

Thus,

m<AOC = m<BOC (bisector property of OC)

m<MOC = m<BOM (congruence property)

m<AOM - m<BOM = m<AOC = m<BOC

m<BOC = m<MOC =
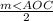`(m<AOC)/(2)` (angle property)

Therefore,

m<AOM > m<BOM (point M location property)

m<MOC =
`(m<AOM - m<BOM)/(2)`