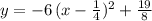Answer:
The vertex form of the equation is:
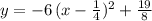
Explanation:
In order to write the equation in vertex form, we need to find the vertex coordinates. The x-coordinate of the vertex of a parabola of the form:

is given by:
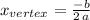
which in our case renders:

Knowing this, then the y-coordinate of the vertex is obtained by using the x-coordinate of the vertex in the functional form:
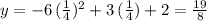
Then, the equation of the parabola in vertex form becomes:

Now we need to find the value of the parameter
 , which since it is the actual leading term of the function in standard form, should be "-6".
, which since it is the actual leading term of the function in standard form, should be "-6".
Then the vertex form of the equation is: