Question

Elwin Osbourne, CIO at GFS, Inc., is studying employee use of GFS e-mail for non-business communications. A random sample of 200 e-mail messages was selected. Thirty of the messages were not business related. The 90% confidence interval for the population proportion is _________.

Answer 1

The 90% confidence interval for the population proportion is

(0.10872, 0.19128)

Step-by-step explanation:

Step-by-step explanation:-

Step(i):-

Given data A random sample of 200 e-mail messages was selected. Thirty of the messages were not business related

Given random sample size 'n' = 200

Given Thirty of the messages were not business related

let 'x' = 30

Probability of the messages were not business related or proportion

`p = (x)/(n) = (30)/(200) = 0.15`

Step(ii):-

The 90% confidence interval for the population proportion is

`(p - Z_(0.10) \sqrt{(p(1-p))/(n) } , p + Z_(0.10) \sqrt{(p(1-p))/(n) } )`

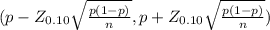
Level of significance ∝ = 0.90 or 0.10

The critical value Z₀.₁₀ = 1.645

The 90% confidence interval for the population proportion is

`( 0.15-1.645 \sqrt{(0.15(1-0.15))/(200) } , 0.15 +1.645 \sqrt{(0.15(1-0.15))/(200) } )`

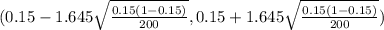
on calculation, we get

(0.15 - 0.04128 , (0.15 + 0.04128)

(0.10872, 0.19128)

Conclusion:-

The 90% confidence interval for the population proportion is

(0.10872, 0.19128)