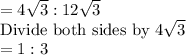Question

An equilateral triangle has sides 8 units long. An equilateral triangle with sides 4 units long is cut off at the top, leaving an isosceles trapezoid. What is the ratio of the area of the smaller triangle to the area of the trapezoid? Express your answer as a common fraction.

Answer 1

1:3

Explanation:

Please study the diagram briefly to understand the concept.

First, we determine the height of the isosceles trapezoid using Pythagoras theorem.

`4^2=2^2+h^2\\h^2=16-4\\h^2=12\\h=√(12)\\ h=2√(3)$ units`

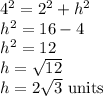
The two parallel sides of the trapezoid are 8 Inits and 4 units respectively.

Area of a trapezoid
`=\frac12 (a+b)h`

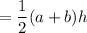
Area of the trapezoid

`=\frac12 (8+4)*2√(3)\\=12√(3)$ Square Units`

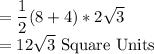
For an equilateral triangle of side length s.

Area
`=(√(3))/(4)s^2`

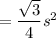
Side Length of the smaller triangle, s= 4 Units

Therefore:

Area of the smaller triangle

`=(√(3))/(4)*4^2\\=4√(3)$ Square units`

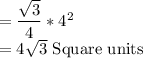
Therefore, the ratio of the area of the smaller triangle to the area of the trapezoid

`=4√(3):12√(3)\\$Divide both sides by 4√(3)\\=1:3`