Answer:
66.992%
Explanation:
![Sales, S(t)=7-6\sqrt[3]{t}](https://img.qammunity.org/2021/formulas/mathematics/college/q41le1x4eg56m2tn99e884fjkpfgx41cdx.png)
Since we want to maximize revenue for the government
Government's Revenue= Sales X Tax Rate
![R(t)=t \cdot S(t)\\R(t)=t(7-6\sqrt[3]{t})\\=7t-6t^(1+1/3)\\R(t)=7t-6t^(4/3)](https://img.qammunity.org/2021/formulas/mathematics/college/cjr3oxyprjg9p4mcszk9ykyiugn74o2d8v.png)
To maximize revenue, we differentiate R(t) and equate it to zero to solve for its critical points. Then we test that this critical point is a relative maximum for R(t) using the second derivative test.
Now:
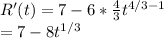
Setting the derivative equal to zero
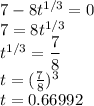
Next, we determine that t=0.6692 is a relative maximum for R(t) using the second derivative test.
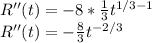
R''(0.6692)=-3.48 (which is negative)
Therefore, t=0.66992 is a relative maximum for R(t).
The tax rate, t that maximizes revenue for the government is:
=0.66992 X 100
t=66.992% (correct to 3 decimal places)