Answer:
90% confidence interval for the population mean
(16.971 , 19.029)
Explanation:
Step(i):-
Given mean of the sample x⁻ = 18 days
Standard deviation of the Population 'σ' = 3 days
Given sample size 'n' =23
Step(ii):-
90% confidence interval for the population mean is determined by
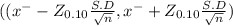
Critical value Z = 1.645
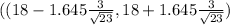
(18 -1.029 , 18 + 1.029)
(16.971 , 19.029)
final answer:-
90% confidence interval for the population mean
(16.971 , 19.029)