Question

Applying Gaussâs Law

When a charge is placed on a metal sphere, it ends up in equilibrium at the outer surface. Use this information to determine the electric field of +3.0 μC charge put on a 5.0-cm aluminum spherical ball at the following two points in space: (a) a point 1.0 cm from the center of the ball (an inside point) and (b) a point 10 cm from the center of the ball (an outside point).

Answer 1

a) E = 0

b) E = 2.697 MN/C

Step-by-step explanation:

Solution:-

- The Gauss Law makes life simpler by allowing us to determine the Electric Field strength ( E ) of symmetrically charged objects. By choosing an appropriate Gaussian surface and determine the flux ( Φ ) that passes through an imaginary closed surface.

- The Law states that the net flux ( Φ ) that passes through a Gaussian surface is proportional to the net charged ( Q ) stored within that surface. We can mathematically express the flux ( Φ ) as follows:

Φ = Q / εo

Where, 1 / εo : The proportionality constant

εo: The permittivity of free space = 8.85*10^-12

- The flux produced by a charged object is also given in form of a surface integral of Electric Field ( E ) over the entire surface area ( A ) of the Gaussian surface as follows:

Φ =
`_S\int\int [ E ] . dA`

- We can combine the two relations as follows:

`_S\int\int [ E ] . dA` = Q / εo

- Now we will consider a charged metal sphere. The important part to note is that the charge on a conducting sphere ( Q ) uniformly distributed on the outside surface of the charged sphere.

- Lets consider a case, where we set up our Gaussian surface ( spherical ) with radius ( r ) < radius of the charged metal surface ( a ). We will use the combined relation and determine the Electric Field ( E ) within a charged metal sphere as follows:

`E. ( 4\pi*r^2 ) = (Q_e_n_c)/(e_o) \\\\E = (Q_e_n_c)/(e_o4\pi*r^2)`

- However, the amount of charge enclosed in our Gaussian surface is null or zero. As all the charge is on the surface r = a. Hence (Q_enc = 0 ),

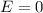`E = 0` ..... ( r < a )

- For the case when we set up our gaussian surface with radius ( r ) > radius of the charged metal surface ( a ). We placed a charge of Q = +3.0uC on the surface of the metal sphere. Therefore, the electric field strength at a distance ( r ) from the center of metal sphere is:

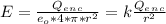`E = (Q_e_n_c)/(e_o*4*\pi*r^2 ) = k(Q_e_n_c)/(r^2 )` .... ( r > a )

- The above relation turns out to be the Electric Field strength ( E ) produced by a point charge at distance ( r ) from the center. Where, k = 8.99*10^9 is the Coulomb's constant.

a) The radius of the charged metal sphere is given to be a = 5.0 cm. The first point r = 1.0 cm lies within the metal sphere. We looked at the first case where, ( r < a ) the enclosed charge is zero. Hence, the magnitudue of Electric Field Strength ( E ) is zero. ( E = 0 )

b) The second point lies at 10 cm from the center. For this we will use the second case where, ( r > a ). The Electric Field Strength due to a point charge with an enclosed charge of Q = +3.0 uC is:

`E = ( 8.99*10^9 ) * (3.0*10^-^6)/(0.1^2) \\\\E = 2697000 N / C`

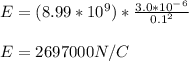
Answer: The electric field strength at point 10 cm away from the center is 2.697 MN/C