Answer:
the speed N of the grinding wheel after 5 complete revolutions of the handle starting from rest is 3122.62 rev/min
Step-by-step explanation:
From the given information ;
According to the principles of Conservation of energy;
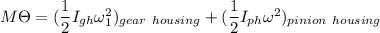
where;
 gain in potential energy as a result of restoring friction
gain in potential energy as a result of restoring friction
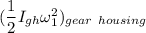 = kinetic energy as a result of rotation of the gear housing
= kinetic energy as a result of rotation of the gear housing
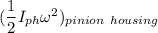 = Kinetic energy as a result of rotation of pinion housing
= Kinetic energy as a result of rotation of pinion housing
However; the equation can be re-written as:
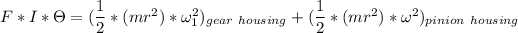
where;
F = restoring Force
I = mass moment of the inertia
r = radius of gyration
Let assume the mass moment of inertia is 6.0 In around the the handle of the hand-operated grinder, since it is not given and a diagram is not attached ;
NOW;
![4.0*(6.0)/(12)*5*2 \pi =[ ((1)/(2)*((4.26)/(32.2))*((2.97)/(12))^2*((\omega)/(5))^2+( (1)/(2))*((1.07)/(33.2)) *((1.95)/(12))^2* \omega ^2)]](https://img.qammunity.org/2021/formulas/engineering/college/3lfumz9ivmjldwtlareexlohusvco76xmn.png)
62.83 =
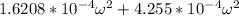
62.83 =
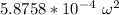

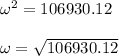
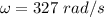
The spinning of the wheel is
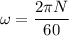

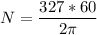
N = 3122.62 rev/min
Thus; the speed N of the grinding wheel after 5 complete revolutions of the handle starting from rest is 3122.62 rev/min