Question

(a) Use the Quotient Rule to differentiate the function f(x)=tan(x)-1/sec(x). f'(x)=

(b) Simplify the expression for f(x) by writing it in terms of sin(x) and cos(x), the find f'(x).

(c) Are your answers to part (a) and (b) equivalent?

For part (a) (which I got correct), I got f'(x)=-sin(x)tan(x)+sec(x)+sin(x)

I got part (b) wrong and I am certain it is a simple thing I am overlooking, but if someone could show me, I would appreciate it.

For part (c) I knew they were equivalent, and the answers is yes.

Answer 1

(a) sin(x) + cos(x)

(b) sin(x) + cos(x)

(c) Both answers are equivalent

Explanation:

(a) The given function is:

`f(x) = (tan(x)-1)/(sec(x))`

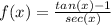
According to the quotient rule:

`f(x) = (g(x))/(h(x))\\f'(x)= (g'(x)h(x)-g(x)h'(x))/(h(x)^2)`

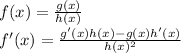
Applying the quotient rule:

`f(x) = (tan(x)-1)/(sec(x))\\f'(x)=(sec^2(x)*sec(x)-(tan(x)-1)*sec(x)tan(x))/(sec(x)^2)\\f'(x)=(sec^3(x)-sec(x)tan^2(x)+sec(x)tan(x))/(sec(x)^2)\\f'(x)=sec(x)+(tan(x)-tan^2(x))/(sec(x))\\ (tan(x))/(sec(x))=sin(x) \\f'(x)=sec(x)+sin(x)-sin(x)tan(x)\\`

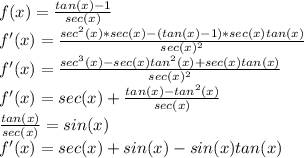
This can be simplified to:

`f'(x)=sec(x)+sin(x)-sin(x)tan(x)\\f'(x) = (1)/(cos(x))+sin(x)-(sin^2(x))/(cos(x))\\f'(x)=(1+sin(x)cos(x)-sin^2(x))/(cos(x))\\f'(x)=(sin^2(x)+cos^2(x)+sin(x)cos(x)-sin^2(x))/(cos(x))\\f'(x)=(cos^2(x)+sin(x)cos(x))/(cos(x))\\ f'(x)=sin(x) +cos(x)`

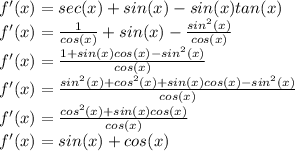
(b) Simplifying in terms of sin(x) and cos(x):

`f(x) = (tan(x)-1)/(sec(x))\\f(x)=((sin(x))/(cos(x))-1 )/((1)/(cos(x)) ) \\f(x)=sin(x)-cos(x)\\f'(x) = cos(x)+sin(x)`

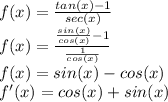
(c) As proven above, both answers are equivalent.