Question

Write a RECURSIVE and EXPLICIT model for the following geometric sequence. 2, 8, 32, 128, 512, ...

Answer 1

Answers:

The recursive model is
`\begin{cases}a_1 = 2\\a_(n) = 4*a_(n-1)\end{cases}`

--------------

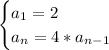
The explicit model is
`a_n = 2(4)^(n-1)`

============================================================

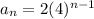
Step-by-step explanation:

Finding the recursive model

The starting term of this geometric sequence is 2. We would write
`a_1 = 2`. The small subscript 1 indicates the term number, while 2 is the term itself.

The second term is
`a_2 = 8`

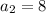
The third term is
`a_3 = 32`

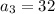
and so on. Pick any term you want that isn't the first term. Divide that term you picked over its previous term. So say you picked the third term. Divide that over the second term to get

(third term)/(second term) = 32/8 = 4

or you could do fourth over third

(fourth term)/(third term) = 128/32 = 4

Each time you do this, you should get 4 as a result. This is the common ratio. We multiply each term by 4 to get the next term.

So the recursive step is
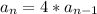`a_(n) = 4*a_(n-1)` which says "the nth term
`a_n` is found by multiplying the prior term
`a_(n-1)` by 4". The entire "n-1" is a subscript to show it is the term just before the nth term.

Overall we have
`a_1 = 2` as the first term and the recursive rule
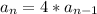`a_n = 4*a_(n-1)` both of which combine to get the recursive model
`\begin{cases}a_1 = 2\\a_(n) = 4*a_(n-1)\end{cases}`

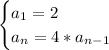
That just says "start at 2, multiply each term by 4 to get the next one"

----------------------------------------------------

Finding the explicit model

We have a = 2 as the first term and r = 4 as the common ratio. Plug those into the nth term of a geometric sequence formula as shown below

`a_n = a*(r)^(n-1)\\\\a_n = 2(4)^(n-1)`

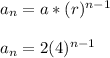
and that's all there is to it.