Question

Yahoo creates a test to classify emails as spam or not spam based on the contained words. This test accurately identifies spam (if it is actually spam) 95% of the time. On the other hand, if an email isn't spam, the test will incorrectly classify it as spam 5% of the time. The prevalence of spam emails is 3 in 10.i) What's the probability that an email picked at random is spam? What's the probability that an email picked at random isn't spam?ii) If you test an email and it reports positive for spam, what is the probability that it is spam? Show your work.iii) If you test an email and it reports negative for spam, what is the probability that it is spam? Show your work.

Answer 1

0.0221

Explanation:

Answer 2

Answer and Step-by-step explanation:

The computation is shown below:

Let us assume that

Spam Email be S

And, test spam positive be T

Given that

P(S) = 0.3

`P((T)/(S)) = 0.95`

`P((T)/(S^c)) = 0.05`

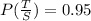
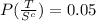
Now based on the above information, the probabilities are as follows

i. P(Spam Email) is

= P(S)

= 0.3

`P(S^c) = 1 - P(S)`

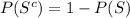
= 1 - 0.3

= 0.7

ii.
`P((S)/(T)) = (P(S\cap\ T)/(P(T))`

`= (P((T)/(S)) . P(S) )/(P((T)/(S)) . P(S) + P((T)/(S^c)) . P(S^c) )`

`= (0.95 * 0.3)/(0.95 * 0.3 + 0.05 * 0.7)`

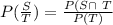
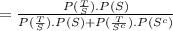
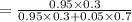
= 0.8906

iii.
`P((S)/(T^c)) = (P(S\cap\ T^c)/(P(T^c))`

`= (P((T^c)/(S)) . P(S) )/(P((T^c)/(S)) . P(S) + P((T^c)/(S^c)) . P(S^c) )`

`= ((1 - 0.95)* 0.3)/( (1 -0.95)0.95 * 0.3 + (1 - 0.05) * 0.7)`

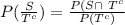
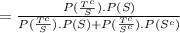
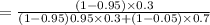
= 0.0221

We simply applied the above formulas so that the each part could come