Question

A bracket ABCD having a hollow circular cross section consists of a vertical arm AB (L 5 6 ft), a horizontal arm BC parallel to the x0 axis, and a horizontal arm CD parallel to the z0 axis (see gure). The arms BC and CD have lengths b1 5 3.6 ft and b2 5 2.2 ft, respectively. The outer and inner diameters of the bracket are d2 5 7.5 in. and d1 5 6.8 in. Aninclined load P 5 2200 lb acts at point D along line DH. Determine the maximum tensile, compressive, and shear stresses in the vertical arm.

Answer 1

The answer is explained below

Step-by-step explanation:

Given that:

1 ft = 0.3048 m, 1 in = 0.0254 m, 1 pound = 4.44822 newton

`b_1=3.6ft=1.1\ m`,
`b_2=2.2 ft=0.67\ m`,
`d_2=7.5 in=0.19\ m`,
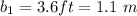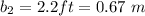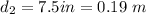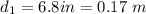`d_1=6.8in=0.17\ m`. P = 2200 lb = 9786 N

The area (A) is given as:

`A=(\pi)/(4) (d_2^2-d_1^2)=(\pi)/(4)(0.19^2-0.17^2)=5.65*10^(-3)m^2`

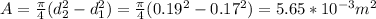
The moment of area is given as:

`l=(\pi)/(64) (d_2^4-d_1^4)=(\pi)/(64)(0.19^4-0.17^4)=2.3*10^(-5)m^4`

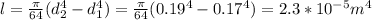
The maximum tensile stress is given as:

`\sigma_1=-(P)/(A)+(M((d_2)/(2) ))/(l) =-(9786\ N )/(5.65*10^(-3)m^2)+(11kNm(0.19 \ m)/2)/(2.3*10^(-5)m^4) =-1.73\ MPa+45.4\ MPa=43.67\ MPa\\\sigma_1=43.67\ MPa`

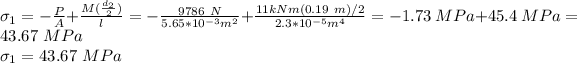
The maximum compressive stress is given as:

`\sigma_c=-(P)/(A)-(M((d_2)/(2) ))/(l) =-(9786\ N )/(5.65*10^(-3)m^2)-(11kNm(0.19 \ m)/2)/(2.3*10^(-5)m^4) =-1.73\ MPa-45.4\ MPa=47.13\ MPa\\\sigma_c=47.13\ MPa`

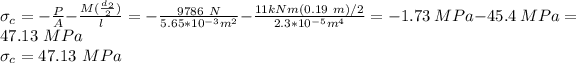
The maximum shear stress is given as:

`\tau_(max)=|(\sigma_c)/(2) |=(47.13\ MPa)/(2)=23.57\ MPa`