Answer:
a+b) The null and alternative hypothesis are:
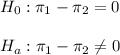
c) Distribution: standard normal distribution.
d) Test statistic z = -2.9398.
e) P-value = 0.0033.
This P-value shows the probability of having this outcome (sample results) given that the null hypothesis is true (that there is no difference in the proportions). This low value of the P-value shows that is unlikely that this results is only due to chance, so it works as evidence against the null hypothesis.
f) Attached.
The null hypothesis is rejected, as the P-value is smaller than the significance level.
There is enough evidence to support the claim that there is a significant difference in the use of eReaders by different age groups.
Explanation:
This is a hypothesis test for the difference between proportions.
The claim is that there is a significant difference in the use of eReaders by different age groups.
Then, the null and alternative hypothesis are:
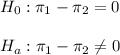
The significance level is 0.05.
The sample 1 (16-29 years old), of size n1=627 has a proportion of p1=0.07.
The sample 2 (30+ years old), of size n2=2314 has a proportion of p2=0.11.
The difference between proportions is (p1-p2)=-0.04.
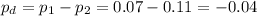
The pooled proportion, needed to calculate the standard error, is:

The estimated standard error of the difference between means is computed using the formula:
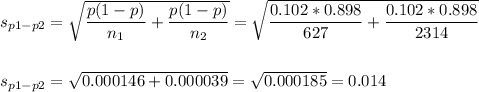
Then, we can calculate the z-statistic as:
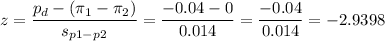
This test is a two-tailed test, so the P-value for this test is calculated as (using a z-table):
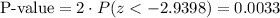
As the P-value (0.0033) is smaller than the significance level (0.05), the effect is significant. This P-value shows the probability of having this outcome (sample results) given that the null hypothesis is true.
The null hypothesis is rejected.
There is enough evidence to support the claim that there is a significant difference in the use of eReaders by different age groups.
If we have used the critical value approach, the critical value for a two-tailed test is zc=±1.96. If the test statistic falls within the range of the critical values, the null hypothesis is failed to be rejected.
In this case, the test statistic is smaller than zc=-1.96, so it falls in the rejection region and the null hypothesis is rejected.