Answer:
a) Null hypothesis:

Alternative hypothesis:
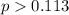
b)
 (1)
(1)
Replacing we got:
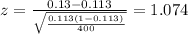
The p value for this case would be given by:
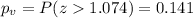
c) For this case we see that the p value is higher than the significance level of 0.05 so then we have enough evidence to FAIL to reject the null hypothesis and we can't conclude that the true proportion workers belonged to unions is significantly higher than 11.3%
Explanation:
Information given
n=400 represent the random sample taken
X=52 represent the workers belonged to unions
 estimated proportion of workers belonged to unions
estimated proportion of workers belonged to unions
 is the value that we want to test
is the value that we want to test
 represent the significance level
represent the significance level
Confidence=95% or 0.95
z would represent the statistic
 represent the p value
represent the p value
Part a
We want to test if the true proportion of interest is higher than 0.113 so then the system of hypothesis are.:
Null hypothesis:

Alternative hypothesis:
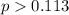
Part b
The statistic is given by:
 (1)
(1)
Replacing we got:
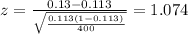
The p value for this case would be given by:
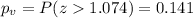
Part c
For this case we see that the p value is higher than the significance level of 0.05 so then we have enough evidence to FAIL to reject the null hypothesis and we can't conclude that the true proportion workers belonged to unions is significantly higher than 11.3%