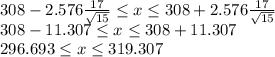Question

Suppose heights of seasonal pine saplings are normally distributed and have a known population standard deviation of 17 millimeters and an unknown population mean. A random sample of 15 saplings is taken and gives a sample mean of 308 millimeters. Find the confidence interval for the population mean with a 99%z0.10 z0.05 z0.025 z0.01 z0.0051.282 1.645 1.960 2.326 2.576

Answer 1

`296.693\leq x\leq 319.307`

Explanation:

The confidence interval for the population mean x can be calculated as:

`x'-z_(\alpha /2)(s)/(√(n) ) \leq x\leq x'+z_(\alpha /2)(s)/(√(n) )`

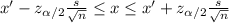
Where x' is the sample mean, s is the population standard deviation, n is the sample size and
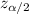`z_(\alpha /2)` is the z-score that let a proportion of
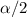`\alpha /2` on the right tail.

`\alpha` is calculated as: 100%-99%=1%

So,
`z_(\alpha/2)=z_(0.005)=2.576`

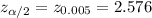
Finally, replacing the values of x' by 308, s by 17, n by 15 and
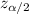`z_(\alpha /2)` by 2.576, we get that the confidence interval is:

`308-2.576(17)/(√(15) ) \leq x\leq 308+2.576(17)/(√(15) )\\308-11.307 \leq x\leq 308+11.307\\296.693\leq x\leq 319.307`