Question

Solve for x.

2/x^2−4 − 1/x+2=3/x−2




−32

−12

23

2

Answer 1

`-(1)/(2)`

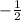
Explanation:

1. Multiply both sides of the equation by the LCM (x - 2)(x + 2):

`(2)/(x^(2) -4) (x-2)(x+2)`

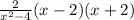
factor x² - 4 by rewriting it as x² - 2²

x² - 2² = (x + 2)(x - 2)

now we have;

`(2)/((x+2)(x-2)) (x-2)(x+2)`

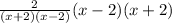
cancel the common factors (x - 2)(x + 2)

= 2

-------------------------------

`(-1)/(x+2) (x-2)(x+2)`

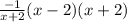
cross cancel the common factor (x + 2)

`(-1)/(x-2)=-(x-2)=-x+2`

-------------------------------

`(3)/(x-2) (x-2)(x+2)`

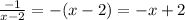
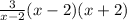
cross cancel the common factor (x - 2)

3(x + 2)

distribute the 3

3x + 6

-------------------------------

combining all new values, we have;

2 + (-x) + 2 = 3x + 6

-x + 4 = 3x + 6

2. Isolate x:

-x + 4-4 = 3x + 6-4

-x = 3x + 2

-x-3x = 3x-3x + 2

-4x = 2

-4x/-4 = 2/-4

x =
`-(1)/(2)`

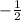
hope this helps!

Answer 2

x = -1/2.

Explanation:

x^2 - 4 = (x - 2)(x + 2) so if we multiply each term by x^2 -4 we get:

2 - 1(x - 2) = 3(x + 2)

2 - x + 2 = 3x + 6

2 + 2 - 6 = 3x + x

4x = -2

x = -1/2.