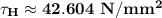Question

The internal shear force V at a certain section of a steel beam is 80 kN, and the moment of inertia is 64,900,000 . Determine the horizontal shear stress at point H, which is located L

Answer 1

Here is the complete question

The internal shear force V at a certain section of a steel beam is 80 kN, and the moment of inertia is 64,900,000 . Determine the horizontal shear stress at point H, which is located L = 20 mm below the centriod

The missing image which is the remaining part of this question is attached in the image below.

Answer:

The horizontal shear stress at point H is
`\mathbf{\tau_H \approx 42.604 \ N/mm^2}`

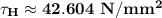
Step-by-step explanation:

Given that :

The internal shear force V = 80 kN = 80 × 10³ N

The moment of inertia = 64,900,000

The length = 20 mm below the centriod

The horizontal shear stress
`\tau` can be calculated by using the equation:

`\tau = (VQ)/(Ib)`

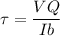
where;

Q = moment of area above or below the point H

b = thickness of the beam = 10 mm

From the centroid ;

Q =
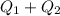
`Q_1 + Q_(2)`

Q =
`A_1y_1 + A_(2)y_(2)`

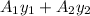
Q = ( ( 70 × 10) × (55) + ( 210 × 15) (90 + 15/2) ) mm³

Q = ( ( 700) × (55) + ( 3150 ) ( 97.5) ) mm³

Q = ( 38500 + 307125 ) mm³

Q = 345625 mm³

`\tau_H = (VQ)/(Ib)`

`\tau_H = (80*10^3 * 345625)/(64900000*10 )`

`\tau_H = (2.765*10^(10))/(649000000 )`

`\tau_H = 42.60400616 \ N/mm^2`

`\mathbf{\tau_H \approx 42.604 \ N/mm^2}`

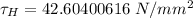
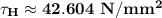
The horizontal shear stress at point H is
`\mathbf{\tau_H \approx 42.604 \ N/mm^2}`