Question

You are standing 5 miles away from the peak. You look up at a 47-degree angle to the peak. How tall is the mountain? Hint: 5280 feet = 1 mile. Round your answer to the nearest foot.

Answer 1

19272 feet

Explanation:

We are given that the distance between the person and peak is 5 miles.

and angle is
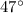`47^\circ` when we look up at the mountain peak.

The given situation is best represented as a right angled triangle as shown in the attached figure.

`\triangle`IKJ where
`\angle K = 90^\circ`

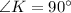
IK is the mountain.

J is the point where we are standing.

Distance JI = 5 miles

`\angle J = 47^\circ`

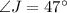
To find: Distance IK = ?

We can use trigonometric identities to find IK.

`sin\theta = (Perpendicular)/(Hypotenuse)`

`sinJ = (IK)/(JI)\\\Rightarrow sin47 = (IK)/(5)\\\Rightarrow IK = sin47^\circ * 5\\\Rightarrow IK = 0.73 * 5\\\Rightarrow IK = 3.65\ miles \\\Rightarrow IK = 3.65 * 5280\ ft\\\Rightarrow IK = 19272\ ft`

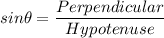
Hence, height of mountain = 19272 ft