Answer:
a) 0.69
The probability that a randomly selected 10-year old child will be more than 51.75 inches tall
P(X>51.75 ) = 0.6915
Explanation:
Step(i):-
Given mean of the Population = 54.6 inches
Given standard deviation of the Population = 5.7 inches
Let 'X' be the random variable of normal distribution
Let 'X' = 51.75 inches
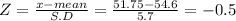
Step(ii):-
The probability that a randomly selected 10-year old child will be more than 51.75 inches tall
P(X>51.75 ) = P(Z>-0.5)
= 1 - P( Z < -0.5)
= 1 - (0.5 - A(-0.5))
= 1 -0.5 + A(-0.5)
= 0.5 + A(0.5) (∵A(-0.5)= A(0.5)
= 0.5 +0.1915
= 0.6915
Conclusion:-
The probability that a randomly selected 10-year old child will be more than 51.75 inches tall
P(X>51.75 ) = 0.6915