Question

The base and sides of a container is made of wood panels. The container does not have a lid. The base and sides are rectangular. The width of the container is x cm. The length is double the width. The volume of the container is 100 cm3. Determine the minimum surface area that this container will have.

Answer 1

106.71 cm²

Explanation:

Let 'h' be the height of the container. If the width is x cm and the length is 2x cm, then the volume and surface area are given by:

`V=x*2x*h=2hx^2\\100=2hx^2\\A=2*(xh)+2*(2x*h)+(2x*x)\\A=6xh+2x^2`

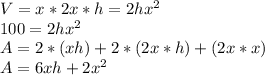
Rewriting the area function as a function of 'x':

`100=2hx^2\\h=(50)/(x^2) \\A=6xh+2x^2\\A=(300)/(x)+2x^2`

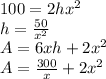
The value of 'x' for which the derivate of the area function is zero, is the one that yields the minimum surface area:

`A=(300)/(x)+2x^2\\(dA)/(dx)=0=(-300)/(x^2)+4x\\4x^3=300\\x=4.217 cm`

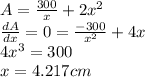
Therefore, the minimum area is:

`A_(min)=(300)/(4.217)+2*(4.217^2) \\A_(min)= 106.71\ cm^2`

The container will have a minimum surface area of 106.71 cm²