Answer : value of x and y in the matrix equation is:
x = -3
y = +4, -4
Step-by-step explanation :
The matrix expression is:
![\left[\begin{array}{ccc}x+4\\y^2+1\end{array}\right]+\left[\begin{array}{ccc}-9x\\-17\end{array}\right]=\left[\begin{array}{ccc}28\\0\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/high-school/7t3hyvq1k51wq6qwgedgjghblck3dqcc3o.png)
First we have to add left hand side matrix.
![\left[\begin{array}{ccc}(x+4)+(-9x)\\(y^2+1)+(-17)\end{array}\right]=\left[\begin{array}{ccc}28\\0\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/high-school/ewtxaer0um069gyolu8z3vqyx3lc96qogk.png)
Now we have to add left hand side terms.
![\left[\begin{array}{ccc}x+4-9x\\y^2+1-17\end{array}\right]=\left[\begin{array}{ccc}28\\0\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/high-school/5brgsi461oy1muwm3cp9ru06ni8mbws07t.png)
![\left[\begin{array}{ccc}4-8x\\y^2-16\end{array}\right]=\left[\begin{array}{ccc}28\\0\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/high-school/9qy8mywyclxueekk1942teghvt2ooy38cs.png)
Now we have to equating left hand side matrix to right hand matrix, we get:
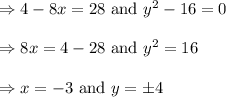
Therefore, the value of x and y in the matrix equation is -3 and +4, -4 respectively.