Question

According to the Center for Disease Control and Prevention (CDC), up to 20% of Americans contract the influenza virus each year, and approximately 3% of all births in the United States result in birth defects each year. Consider two babies being born independently of one another. 1. The probability that both babies have birth defects is;______ a. 0.0009. b. 0.0400.c. 0.0606. d. 0.2000. 2. The probability that neither baby catches the flu in a given year is:_____ a. 0.024. b. 0.040. c. 0.230 d. 0.640. 3. Event A occurs with probability 0.1. Event B occurs with probability 0.6. If A and B are independent, then:______ a. P(A and B) = 0.06. b. P(A or B) = 0.70. c. P(A and B) = 0.70. d. P(A or B) = 0.06. 4. Event A occurs with probability 0.2. Event B occurs with probability 0.9. Event A and B:______ are disjoint cannot be independent. cannot be disjoint. are reciprocating. The center for Disease Control and Prevention reports that the rate of Chlamydia infections among American women ages 20 to 24 is 2791.5 per 100,000. Take a random sample of three American women in this age group. 5. The probability that all of them have a Chlamydia infection is:_____ a. nearly 0. b. 0.028. c. 0.084. d. 0.837 6. The probability that none of them have a Chlamydia infection is:_______ a. 0.084. b. 0.919. c. 0.972. d. nearly 1.

Answer 1

(1) a. 0.0009

(2) d. 0.640

(3)

• a. P(A and B) = 0.06.
• b. P(A or B) = 0.70.

(4)Not disjoint

(5) a. nearly 0.

(6)b. 0.919

Explanation:

(1)Probability of a baby being born with a birth defect =3%=0.03

The probability that both babies have birth defects=0.03 X 0.03= 0.0009.

(2)The probability of contracting the influenza virus each year = 20%=0.2

Therefore, the probability of not contracting the influenza virus =1-0.2=0.8

The probability that neither baby catches the flu in a given year:

=0.8 X 0.8

=0.64

(3)

P(A)=0.1

P(B)=0.6

P(A or B)=P(A)+P(B)=0.1 + 0.6 =0.7

P(A and B)=P(A)XP(B)=0.1 X 0.6 =0.06

(4)

P(A)=0.2

P(B)=0.9

Event A and B cannot be disjoint.

(5)

The probability of an American woman aged 20 to 24 having Chlamydia infection
`=(2791.5)/(100000)`

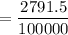
The probability that three randomly selected women in this age group have the infection

`=(2791.5)/(100000) * (2791.5)/(100000) * (2791.5)/(100000) \\\\=0.00002175\\\approx 0`

(6)The probability of an American woman aged 20 to 24 not having Chlamydia infection
`=1-(2791.5)/(100000)`

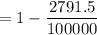
The probability that three randomly selected women in this age group do not have the infection

`=\left(1-(2791.5)/(100000)\right)^3\\\\=0.9186\\\approx 0.919`