Question

Let X denote the amount of time a book on two-hour reserve is actually checked out, and suppose the cdf is the following. F(x) = 0 x < 0 x^2/16 0 ≤ x < 4 1 4 ≤ x Use the cdf to obtain the following. (If necessary, round your answer to four decimal places.)Required:a. Calculate P(x<=1)b. Calculate P(0.5<= x<=1)c. Calculate P(x>1.5)d. What is the media checkout duration μ? e. Obtain the density function f(x)f. Calculate E(X).

Answer 1

Answer: a) P(x≤1) = 0.0625

b) P(0.5≤x≤1) = 0.0468

c) P(x>1.5) = 0.8593

d) Median (m) = 3.4641

e) f(x) = 0 x < 0

x/8 0≤x≤4

0 x≥4

Explanation:

a) To calculate the probability of F(x) with x being less or equal 1 is:

P(x≤1) = F(1)

F(1) =
`(1^(2))/(16)`

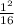
P(x≤1) = 0.0625

b) To calculate probability of F(x) with x being between 0.5 and 1:

P(0.5≤x≤1) = F(x≤1) - F(x≤0.5) = F(1) - F(0.5)

F(1) = 0.0625

F(0.5) =
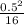`(0.5^(2))/(16)` = 0.0156

P(0.5≤x≤1) = 0.0625 - 0.0156

P(0.5≤x≤1) = 0.0468

c) P(x>1.5) = 1 - P(x≤1.5) = 1 - F(1.5)

F(1.5) = 0.1406

P(x>1.5) = 1 - 0.1406

P(x>1.5) = 0.8593

d) Median is a point in the graph that divides it in half, so to determine the point, here called m:

`\int\limits^m_0 {(x^(2))/(16) } \, dx = (1)/(2)`

`(1)/(16)\int\limits^m_0 {x^(2)} \, dx = (1)/(2)`

`\int\limits^m_0 {x^(2)} \, dx = 8`

`(x^(3))/(3) = 8`

`(m^(3))/(3) - 0 = 8`

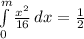
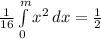
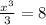
m³ = 24

m = 3.4641

The median checkout duration is 3.4641 hours.

e) Density function of a cumulative distribution function (cdf) as well as in a continuous random variable is the first derivative of a function. Then, for this function it is:

f(x) = F'(x)

f(x) = 0 x<0

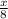`(x)/(8)` 0≤x≤4

0 x≥4

f) E(X) =
`\int\limits^4_0 {x}f(x) \, dx`

=
`\int\limits^4_0 {x}.(x)/(8) \, dx`

=
`\int\limits^4_0 {(x^(2))/(8) \, dx`

=
`(x^(3))/(24)`

=
`(4^(3))/(24) - (0^(3))/(24)`

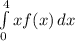
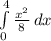
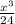
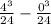
E(X) = 2.6667