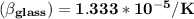Question

A glass flask whose volume is 1000 cm^3 at a temperature of 1.00°C is completely filled with mercury at the same temperature. When the flask and mercury are warmed together to a temperature of 52.0°C , a volume of 8.50 cm^3 of mercury overflows the flask.Required:If the coefficient of volume expansion of mercury is βHg = 1.80×10^−4 /K , compute βglass, the coefficient of volume expansion of the glass. Express your answer in inverse kelvins.

Answer 1

the coefficient of volume expansion of the glass is
`\mathbf{ ( \beta_(glass) )= 1.333 *10^(-5) / K}`

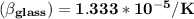
Step-by-step explanation:

Given that:

Initial volume of the glass flask = 1000 cm³ = 10⁻³ m³

temperature of the glass flask and mercury= 1.00° C

After heat is applied ; the final temperature = 52.00° C

Temperature change ΔT = 52.00° C - 1.00° C = 51.00° C

Volume of the mercury overflow = 8.50 cm^3 = 8.50 × 10⁻⁶ m³

the coefficient of volume expansion of mercury is 1.80 × 10⁻⁴ / K

The increase in the volume of the mercury = 10⁻³ m³ × 51.00 × 1.80 × 10⁻⁴

The increase in the volume of the mercury =
`9.18*10^(-6) \ m^3`

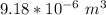
Increase in volume of the glass = 10⁻³ × 51.00 ×
`\beta _(glass)`

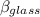
Now; the mercury overflow = Increase in volume of the mercury - increase in the volume of the flask

the mercury overflow =
`(9.18*10^(-6) - 51.00* \beta_(glass)*10^(-3))\ m^3`

`8.50*10^(-6) = (9.18*10^(-6) -51.00* \beta_(glass)* 10^(-3) )\ m^3`

`8.50*10^(-6) - 9.18*10^(-6) = ( -51.00* \beta_(glass)* 10^(-3) )\ m^3`

`-6.8*10^(-7) = ( -51.00* \beta_(glass)* 10^(-3) )\ m^3`

`6.8*10^(-7) = ( 51.00* \beta_(glass)* 10^(-3) )\ m^3`

`(6.8*10^(-7))/(51.00 * 10^(-3))= ( \beta_(glass) )`

`\mathbf{ ( \beta_(glass) )= 1.333 *10^(-5) / K}`

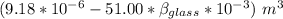
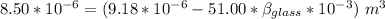
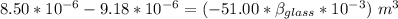
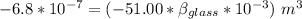
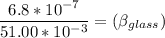
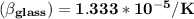
Thus; the coefficient of volume expansion of the glass is
`\mathbf{ ( \beta_(glass) )= 1.333 *10^(-5) / K}`