Question

The average height of students at UH from an SRS of 12 students gave a standard deviation of 2.5 feet. Construct a 95% confidence interval for the standard deviation of the height of students at UH. Assume normality for the data.a. (1.271, 6.245)b. (0.771, 10.245)c. (1.771, 4.245)d. (7.771, 9.245)e. (4.771, 10.245)f. None of the above

Answer 1

c. [1.771;4.245] feet

Explanation:

Hello!

The variable of interest is

X: height of a student at UH

X~N(μ;σ²)

You have to estimate the population standard deviation using a 95% confidence interval.

The statistic to use for the interval is a student Chi-Square with n-1 degrees of freedom. First you have to calculate the CI for the population variance:

`[((n-1)S^2)/(X^2_(n-1;1-\alpha /2)) ;((n-1)S^2)/(X^2_(n-1;\alpha /2)) ]`

`X^2_(n-1;1-\alpha /2)= X^2_(11;0.975)= 21.920`

`X^2_(n-1;\alpha /2)= X^2_(11;0.025)= 3.816`

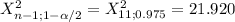
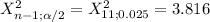
n=12

S= 2.5

`[(11*6.25)/(21.920) ;(11*6.25)/(3.816)} ]`

[3.136; 18.016] feet²

Then you calculate the square root of both limits to get the CI for the population standard deviation:

[√3.136; √18.016]

[1.771;4.245] feet

I hope this helps!