Question

Three equal point charges, each with charge 1.45 μCμC , are placed at the vertices of an equilateral triangle whose sides are of length 0.700 mm . What is the electric potential energy UUU of the system? (Take as zero the potential energy of the three charges when they are infinitely far apart.)

Answer 1

U = 80.91 J

Step-by-step explanation:

In order to calculate the electric potential energy between the three charges you use the following formula:

`U=k(q_1q_2)/(r_(1,2))` (1)

k: Coulomb's constant = 8.98*10^9Nm^2/C^2

q1: q2 charge

r1,2: distance between charges 1 and 2.

For the three charges you have:

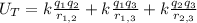`U_T=k(q_1q_2)/(r_(1,2))+k(q_1q_3)/(r_(1,3))+k(q_2q_3)/(r_(2,3))` (2)

You use the fact that q1=q2=q3=q and that the distance between charges are equal. Then, in the equation (2) you have:

q = 1.45μC = 1.45*10^-6C

r = 0.700mm = 0.700*10^-3m

`U_T=3k(q^2)/(r)=3(8.98*10^9Nm^2/C^2)((1.45*10^(-6)C))/(0.700*10^(-3)m)\\\\U_T=80.91J`

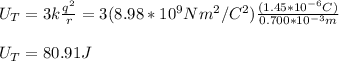
The electric potential energy between the three charges is 80.91 J