Question

Repair calls are handled by one repairman at a photocopy shop. Repair time, including travel time, is exponentially distributed, with a mean of 1.6 hours per call. Requests for copier repairs come in at a mean rate of 2.1 per eight-hour day (assume Poisson).

a. Determine the average number of customers awaiting repairs. (Round your answer to 2 decimal places.)
Number of customers
b. Determine system utilization. (Round your answer to the nearest whole percent. Omit the "%" sign in your response.)
System utilization %
c. Determine the amount of time during an eight-hour day that the repairman is not out on a call. (Round your answer to 2 decimal places.)
Amount of time hoursd. Determine the probability of two or more customers in the system. (Do not round intermediate calculations. Round your answer to 4 decimal places.)
Probability

Answer 1

To calculate the average number of customers awaiting repairs, divide the arrival rate by the service rate. The system utilization is the fraction of time the repairman is busy servicing customers. To find the probability of two or more customers in the system, use the steady-state probability formula.

Step-by-step explanation:

a. To determine the average number of customers awaiting repairs, we need to calculate the arrival rate and the service rate. The arrival rate is given as 2.1 requests per eight-hour day, which means the arrival rate per hour is 2.1 divided by 8. The service rate can be found from the mean repair time, which is 1.6 hours per call. The service rate is the reciprocal of the mean repair time. Using these values, we can calculate the average number of customers awaiting repairs using the formula:

Average number of customers = (Arrival rate)/(Service rate - Arrival rate)

b. The system utilization can be calculated by dividing the arrival rate by the service rate. This will give us the fraction of time the repairman is busy servicing customers.

c. The amount of time during an eight-hour day that the repairman is not out on a call can be calculated by subtracting the total service time from the eight-hour day.

d. The probability of two or more customers in the system can be found using the formula for the steady-state probability:

P(n >= 2) = (Arrival rate^2)/(Service rate*(Service rate - Arrival rate))

Answer 2

the average number of customers awaiting repairs = 0.30

the system utilization = 42

the amount of time that the repairman is not out on a call is = 4.64 hours

the probability of two or more customers in the system = 0.1764

Step-by-step explanation:

Given that :

Repair time, including travel time = mean of 1.6 hours per call.

Requests for copier repairs = mean rate of 2.1 per eight-hour day

i.e mean rate R = 2.1/day

Time = 8 hours

thus; mean rate μ = 8 hours/ 1.6 hours = 5

(a)

Let the average number of customers awaiting repairs be
`I_i` :

`I_i = (R^2)/(\mu (\mu-R))`

`I_i = (2.1^2)/(5 (5-2.1))`

`I_i = (4.41)/(5 (2.9))`

`I_i = (4.41)/(14.5)`

`\mathbf{I_i = 0.30}`

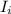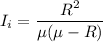
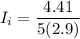
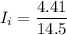
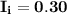
the average number of customers awaiting repairs = 0.30

(b) Determine system utilization.

The system utilization is determined as follows:

`\delta = (R)/(\mu)`

`\delta = (2.1)/(5)`

`{\delta = 0.42}`

`\mathbf{\delta = 42}`

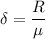
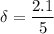
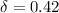
(c) The amount of time during an eight-hour day that the repairman is not out on a call is calculated as :

Percentage of Idle time = 1 -
`\delta`

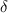
Percentage of Idle time = 1 - 0.42

Percentage of Idle time = 0.58

However during an 8 hour day; The amount of time that the repairman is not out on a call is = 0.58 × 8 = 4.64 hours

(d)

the probability of two or more customers in the system by assuming Poisson Distribution is:

P(N ≥ 2) = 1 - (P₀+ P₁)

where;

P₀ = 0.58

P₁ = 0.58 × 0.42 = 0.2436

P(N ≥ 2) = 1 - ( 0.58 + 0.2436)

P(N ≥ 2) = 1 - 0.8236

P(N ≥ 2) = 0.1764

Thus; the probability of two or more customers in the system is 0.1764