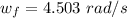Question

A child of mass 46.2 kg sits on the edge of a merry-go-round with radius 1.9 m and moment of inertia 130.09 kg m2 . The merrygo-round rotates with an angular velocity of 2.4 rad/s. The child then walks towards the center of the merry-go-round and stops at a distance 0.779 m from the center. Now what is the angular velocity of the merry-go-round

Answer 1

The angular velocity is
`w_f = 4.503 \ rad/s`

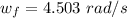
Step-by-step explanation:

From the question we are told that

The mass of the child is
`m_c = 46.2 \ kg`

The radius of the merry go round is
`r = 1.9 \ m`

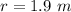
The moment of inertia of the merry go round is
`I_m = 130.09 \ kg \cdot m^2`

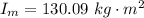
The angular velocity of the merry-go round is
`w = 2.4 \ rad/s`

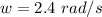
The position of the child from the center of the merry-go-round is
`x = 0.779 \ m`

According to the law of angular momentum conservation

The initial angular momentum = final angular momentum

So

`L_i = L_f`

=>
`I_i w_i = I_fw_f`

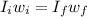
Now
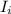`I_i` is the initial moment of inertia of the system which is mathematically represented as

`I_i = I_m + I_(b_1)`

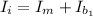
Where
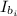`I_(b_i)` is the initial moment of inertia of the boy which is mathematically evaluated as

`I_(b_i) = m_c * r`

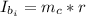
substituting values

`I_(b_i) = 46.2 * 1.9^2`

`I_(b_i) = 166.8 \ kg \cdot m^2`

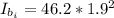
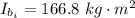
Thus

`I_i =130.09 + 166.8`

`I_i = 296.9 \ kg \cdot m^2`

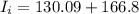
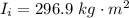
Thus

`I_i * w_i =L_i= 296.9 * 2.4`

`L_i = 712.5 \ kg \cdot m^2/s`

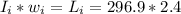
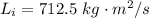
Now

`I_f = I_m + I_(b_f )`

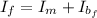
Where
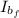`I_(b_f)` is the final moment of inertia of the boy which is mathematically evaluated as

`I_(b_f) = m_c * x`

substituting values

`I_(b_f) = 46.2 * 0.779^2`

`I_(b_f) = 28.03 kg \cdot m^2`

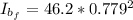
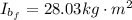
Thus

`I_f = 130.09 + 28.03`

`I_f = 158.12 \ kg \ m^2`

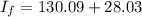
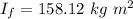
Thus

`L_f = 158.12 * w_f`

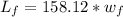
Hence

`712.5 = 158.12 * w_f`

`w_f = 4.503 \ rad/s`